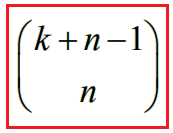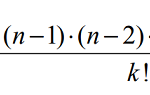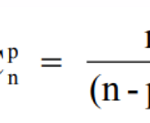Combinazioni con ripetizione

Supponiamo di partire da un insieme di n oggetti, con l’intenzione di creare dei gruppi in ciascuno dei quali siano presenti k oggetti, “pescati” dall’insieme degli n oggetti dati, con la possibilità, fissato un oggetto, di utilizzarlo nessuna volta, una volta, o anche più volte.

Insomma:

gli oggetti della k-upla, che è pensata NON ordinata, non devono essere necessariamente tutti distinti.

In questo contesto, può essere

k <n,
k = n,
k >n 

Queste k-uple non ordinate saranno chiamate le “combinazioni con ripetizione, degli n oggetti dati, di classe k”.

Vediamo degli  esempi:

Esempio

Dato l’insieme delle 4 lettere {A, B, C, D} , le loro combinazioni con ripetizione, di classe 3, sono

BCD, ACD, ABD, ABC, AAA, BBB, CCC, DDD, AAB, AAC, AAD, ABB, BBC, BBD, ACC, BCC, CCD, ADD, BDD, CDD

Problema 1 
Almeno una biglia per contenitore
11 biglie identiche fra loro vanno disposte in 4 contenitori A,B,C,D facendo in modo che nessun contenitore resti vuoto. In quanti modi è possibile distribuire le biglie?

Soluzione

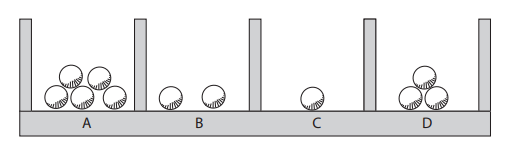
Mettiamo le 11 biglie in fila, come mostrato in basso.

Per scegliere quante biglie mettere in A, quante in B, in C e in D, possiamo utilizzare 3 bastoncini da frapporre fra le sferette a creare 4 gruppi.

In basso è mostrato come esempio la seguente distribuzione: 5 biglie in A, 2 in B, 1 in C e 3 in D.

Evidentemente qualsiasi posizionamento dei tre bastoncini rappresenta in modo univoco una diversa ripartizione e, viceversa, ogni possibile ripartizione può essere rappresentata tramite i 3 bastoncini. Il problema può quindi essere ripensato come un posizionamento di 3“interruzioni” tra le biglie. Con 11 biglie esistono 10 interstizi, per cui il nuovo problema è:

In quanti modi si possono scegliere 3 diverse posizioni su 10 possibili?

La sequenza bastoncino Sì / bastoncino No può essere rappresentata dal disegno in basso:

o più comodamente dalla “parola” xxxxBxBBxx. Ad ogni anagramma corrisponde un diverso posizionamento dei bastoncini e quindi una diversa ripartizione di biglie, per cui, ragionando in termini di permutazioni con ripetizione la soluzione è

Più elegantemente, il problema di scegliere 3 caselle su 10 può essere interpretato come combinazione semplice, fornendo la soluzione (equivalente alla precedente):

E’ utile generalizzare quanto visto al caso di n biglie con k contenitori a disposizione. Procedendo come sopra dovremmo mettere k −1 bastoncini nei n −1 interstizi.

La soluzione è quindi:

Passsiamo ora al seguente

Problema 2

Biglie e contenitori senza restrizione
7 biglie identiche fra loro vanno disposte in 4 contenitori A,B,C,D (volendo si potrebbero anche mettere tutte in A).

In quanti modi è possibile distribuire le biglie?

Soluzione

Invece di iniziare daccapo, partiamo dal problema 1 appena risolto. Ciascuna delle

soluzioni rappresentava una distribuzione di 11 biglie nelle quattro scatole A,B,C,D, con la condizione che in ogni scatola vi fosse almeno una biglia.

Prendiamo una qualsiasi di queste configurazioni e togliamo una biglia per scatola (vedi l’esempio in basso).

Quella che si ottiene sarà ora una ripartizione compatibile con il problema 2: infatti adesso le biglie sono 7 e non si può escludere che qualche scatola sia vuota. Si può anche ragionare in maniera opposta, prendendo una distribuzione compatibilie con il problema 2 e aggiungere una biglia per contenitore: le biglie tornano ad essere 11 con la certezza che nessuna scatola resterà vuota.
Questo discorso dovrebbe convincerci che i problemi 1 e 2 descrivono sostanzialmente la stessa questione e hanno necessariamente la stessa soluzione. Indicati quindi con n il numero di biglie di un problema di tipo 1 (restrizione di 1 biglia per scatola), con N il numero di biglie di un problema ad esso associato di tipo 2 (alcune scatole possono anche essere vuote) e con k il numero di contenitori, si ha la relazione

N =n − k (nell’esempio precedente 7 = 11 − 4)

e quindi n  = N +k .

Possiamo allora dire che la soluzione al problema 2 con N biglie e k contenitori è

Teorema sulle combinazioni con ripetizione

Il numero di combinazioni con ripetizione di k elementi di un insieme I composto da n oggetti distinti è: